First Class Info About In Which Every Node Is Connected To Other
Understanding Complete Graphs
1. What Makes a Graph 'Complete,' Anyway?
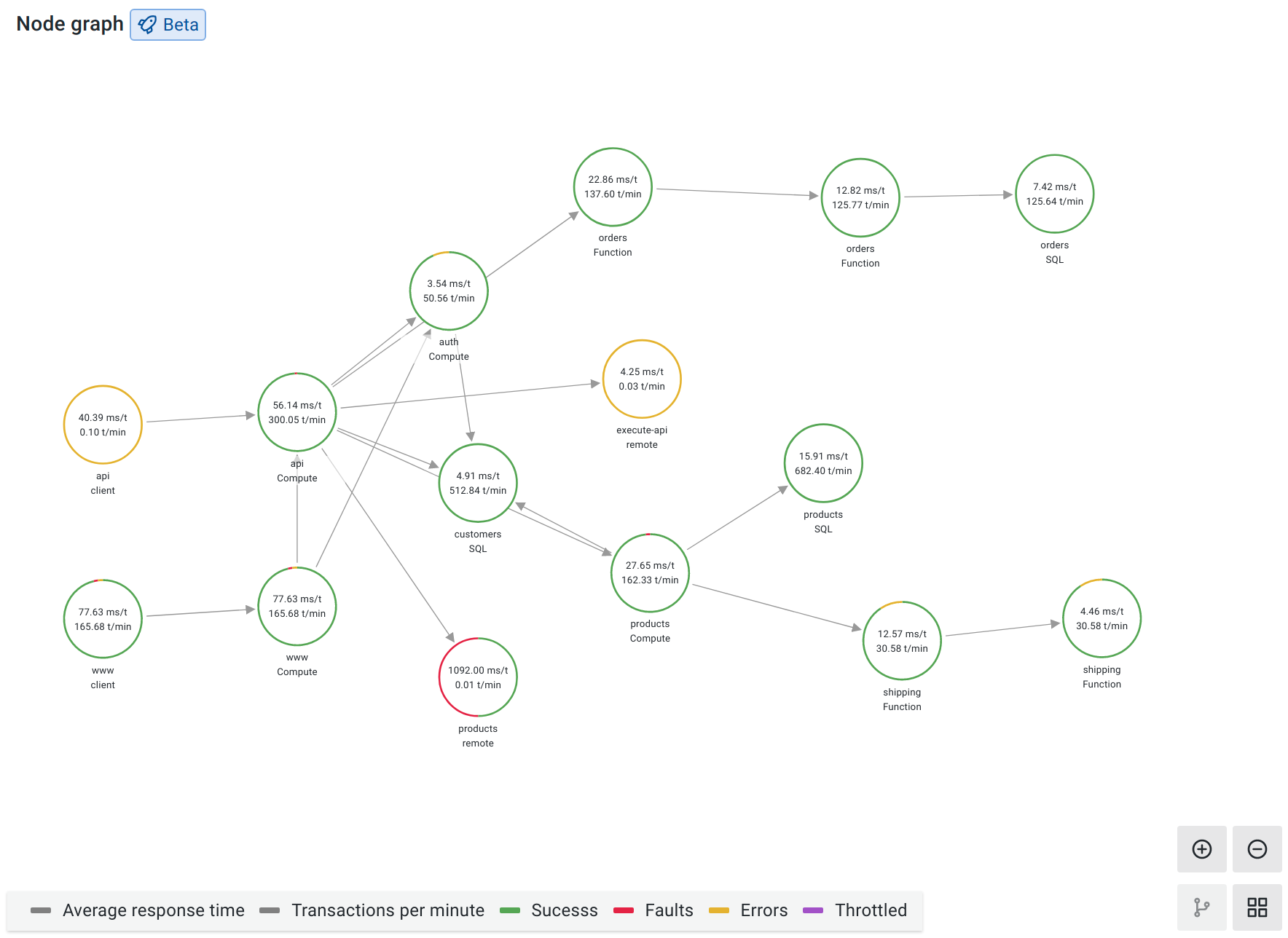
Ever imagine a social network where everyone is friends with everyone else? That's kind of what a complete graph is like in the world of graph theory. Simply put, a complete graph is one "in which every node is connected to every other node." Think of it as the ultimate in networking; no lonely nodes left out in the cold!
In mathematical terms, this means that for 'n' nodes in the graph, each node has a direct connection (an edge) to the remaining 'n-1' nodes. This simple rule leads to some pretty interesting properties and applications, which we'll explore.
But why should you care? Well, understanding complete graphs can help you model various real-world scenarios, from the structure of a tightly-knit team to the organization of interconnected computer networks. Plus, it's a fundamental concept in computer science, so having a grasp of it can be quite beneficial.
It's a bit like that old saying, "It's not what you know, but who you know." In a complete graph, the "who" and the "know" are the same for everyone. Each element has a direct line to all the others.
Visualizing the Network
2. Identifying Characteristics
So, how do you tell if you're looking at a complete graph? Easy! Check if every single node has a direct connection to all the other nodes in the graph. No exceptions! If you find even one node that's not connected to everyone else, then it's not a complete graph. It's like a party where one person is hiding in the corner, refusing to mingle.
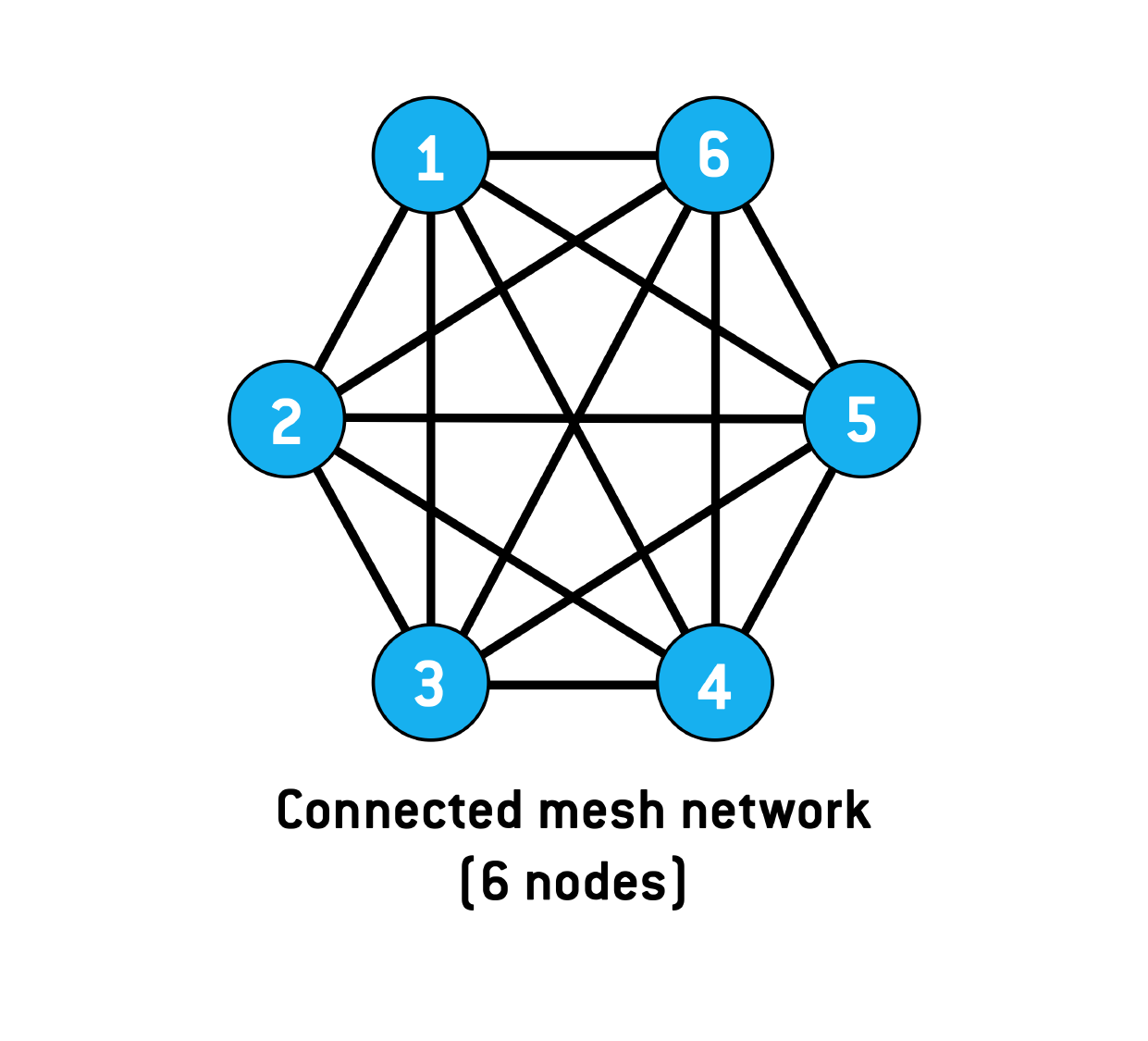
Let's say you have a graph with five nodes (let's call them A, B, C, D, and E). For it to be a complete graph, A must be connected to B, C, D, and E. B must be connected to A, C, D, and E, and so on for each node. If even one of these connections is missing, the whole thing falls apart.
Another way to think about it is to count the edges. A complete graph with 'n' nodes has n(n-1)/2 edges. This formula is handy for quickly checking if a graph is complete, especially if you have a lot of nodes.
Keep an eye out for diagrams of different graphs. If you see a perfect web of connections, with lines crisscrossing every which way, you might just have spotted a complete graph in the wild! It's the 'everyone knows everyone' of the graph world.

Properties and Implications
3. The Power of Full Connectivity
Complete graphs aren't just pretty pictures; they have some fascinating properties. For starters, they're maximally connected, meaning they have the highest possible number of connections for a given number of nodes. This makes them incredibly robust; removing a few connections won't break the graph apart completely.
Another interesting aspect is that any other graph with the same number of nodes can be considered a subgraph of a complete graph. In other words, a complete graph contains all possible connections, so any other graph is just a subset of those connections.
The degree of each node in a complete graph is also significant. Each node has a degree of 'n-1', where 'n' is the number of nodes. This means every node is connected to every other node, making the graph highly efficient for communication or information transfer.
Imagine using a complete graph to model a computer network. Because every computer is directly connected to every other computer, data can be transferred very quickly and reliably. It's like having a direct line to everyone, bypassing the need for intermediaries.
What Is Node In Computer Network Types And Functions
Real-World Applications
4. From Social Networks to Computer Networks
Okay, so complete graphs are cool in theory, but where do you actually see them in the real world? While a perfectly complete graph is rare, the concept helps us understand how networks function. Think about a small, tightly-knit team where everyone communicates directly with each other. That's a near-complete graph in action.
In computer networking, while not perfectly complete due to scalability issues, the idea of full connectivity is essential for ensuring reliable communication within a localized segment of a network. This ensures that information can be shared quickly and efficiently between devices.
Consider social networks, too. While not everyone is connected to everyone else (thank goodness!), the algorithms that suggest friends and connections often rely on the concept of finding "near-complete" clusters of connected individuals. These clusters form the basis of online communities and influence the spread of information.
Even in theoretical physics, complete graphs can be used to model interactions between particles in a system. The connections represent the forces between the particles, and the complete graph represents a state of maximum interaction.
Complete Graphs and Algorithms
5. The Algorithmic Angle
Complete graphs also play a role in algorithms. For example, some graph algorithms become significantly simpler when applied to complete graphs because the connections are already known. This can speed up computations and make analysis easier.
One such application is in clustering algorithms. Identifying complete subgraphs (also known as cliques) within a larger graph can help to find groups of tightly-connected nodes. This is used in social network analysis, where cliques can represent communities of users with shared interests or relationships.
Also, algorithms for finding shortest paths within a graph become trivial in complete graphs. Since every node is directly connected to every other node, the shortest path between any two nodes is simply the direct connection between them.
The predictability and defined structure of complete graphs can be leveraged to build simpler and more efficient algorithms in certain contexts. While the idea of a truly complete graph at large scale isn't practical, its principles help make important optimizations in smaller, manageable networks.
