Underrated Ideas Of Tips About What Are The 5 Basic Integration Formulas
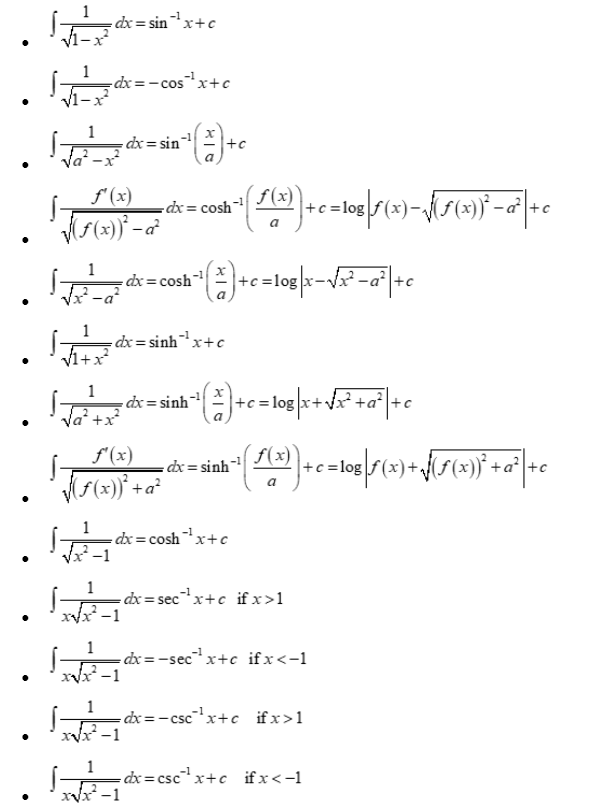
Integration
Unlocking the Secrets of Integration
1. The Foundation of Calculus
Alright, let's talk integration. It's often seen as the boogeyman of calculus, lurking in the shadows and scaring students witless. But fear not! Integration is simply the reverse process of differentiation. Think of it like finding the area under a curve — a pretty useful skill in many fields, from engineering to economics. Now, before you start hyperventilating, know that mastering integration is all about understanding the basics. We're going to delve into five fundamental formulas that form the bedrock of integration. Grasp these, and you'll be well on your way to becoming an integration ninja!
Imagine you're baking a cake. You can't just throw ingredients together and hope for the best, right? You need a recipe, a set of fundamental steps to follow. Similarly, with integration, you need a solid foundation of formulas. These formulas act like the essential ingredients in your integration recipe book. Without them, you're just flailing around, trying to guess the answer, which is never a good strategy when facing a calculus exam. Trust me, I've been there, and it wasn't pretty.
These five formulas are your gateway to understanding more complex integration techniques. They provide the building blocks for solving a vast array of integration problems. They will arm you with the confidence to tackle any integral thrown your way. Forget memorizing dozens of obscure rules; focus on truly grasping these five, and you'll be surprised at how far you can go. Plus, understanding the underlying principles makes the whole process less intimidating and, dare I say, even enjoyable. (Okay, maybe not enjoyable for everyone, but certainly less painful!)
Before diving in, it's important to remember that integration is about more than just finding the antiderivative. It's about understanding accumulation, area, and change. It's a powerful tool for modeling real-world phenomena. So, as we explore these formulas, try to keep the bigger picture in mind. Think about how these concepts relate to your everyday life and the world around you. You might be surprised at how often integration pops up in unexpected places.
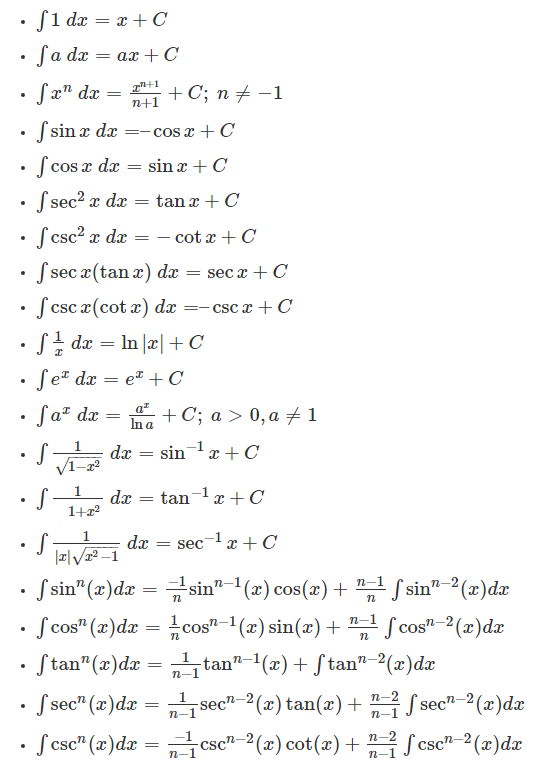
Integration
Formula 1
2. Power Up Your Integrals
First up, we have the power rule. This one is a workhorse and probably the most frequently used formula in integration. It's like the Swiss Army knife of integration techniques! The formula states: xn dx = (xn+1)/(n+1) + C, where n -1 and C is the constant of integration. Don't forget that "+ C"; it's crucial! This rule tells us how to integrate terms of the form x raised to some power.
So, how does it work? Simple. You increase the exponent by one, divide by the new exponent, and add the constant of integration. It's like a reverse version of the power rule for differentiation. Remember that "+ C" represents an arbitrary constant because the derivative of a constant is always zero. This means that when we integrate, we have an infinite number of possible antiderivatives, each differing by a constant. So always, always, always add that "+ C"! I can't stress this enough; it's a very common mistake.
Let's look at an example. Suppose we want to integrate x2. Using the power rule, we increase the exponent by one to get 3 and divide by 3. So, x2 dx = (x3)/3 + C. Easy peasy, right? Another example, x5 dx = (x6)/6 + C. This rule even works for fractional exponents. For example, x dx = x1/2 dx = (x3/2)/(3/2) + C = (2/3)x3/2 + C. Just be mindful of that one exception: n cannot be -1. We'll tackle that case in the next formula.
The power rule is fundamental because it underlies many other integration techniques. It can be used in conjunction with other rules and identities to solve more complex integrals. It's important to practice using the power rule on a variety of examples to become comfortable with it. Don't be afraid to experiment and try different values of 'n'. The more you practice, the more intuitive it will become. Remember, even calculus superheroes started somewhere.
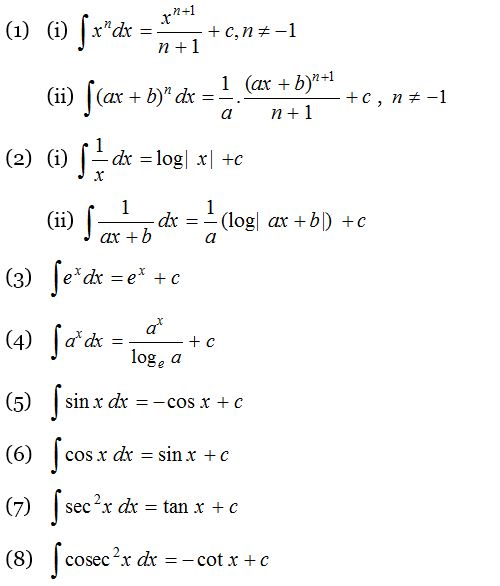
Formula 2
3. A Special Case, Logarithmically Speaking
Now, what happens when n = -1 in the power rule? That's when we need a different formula. The integral of 1/x (or x-1) is the natural logarithm of the absolute value of x. Mathematically, (1/x) dx = ln|x| + C. Notice the absolute value signs! They're important because the natural logarithm is only defined for positive values. Without the absolute value, we'd be limiting our solution to only positive x values, which wouldn't be the full picture.
Why is this the case? Recall that the derivative of ln(x) is 1/x. So, it makes sense that the integral of 1/x is ln(x). But what about negative values of x? Well, the derivative of ln(-x) is also 1/x. That's where the absolute value comes in, ensuring that we cover both positive and negative values of x. Thinking about it this way can really help to understand why the absolute value is so vital in this particular formula.
An example will illustrate the usefulness. Suppose we want to integrate (2/x) dx. We can pull the constant 2 out of the integral, so we have 2(1/x) dx = 2ln|x| + C. That's it! It's a straightforward application of the formula. But don't underestimate its importance. The integral of 1/x appears frequently in various applications, especially when dealing with exponential growth and decay.
This formula is like that one specific tool in your toolbox that you only need occasionally, but when you do, it's absolutely essential. It's not as versatile as the power rule, but it's crucial for handling integrals involving the reciprocal of x. So, make sure you have it memorized and understand why it works. Don't just blindly apply the formula; think about the underlying logarithm and its properties. The better your understanding, the easier it will be to recognize and apply this formula in different contexts.
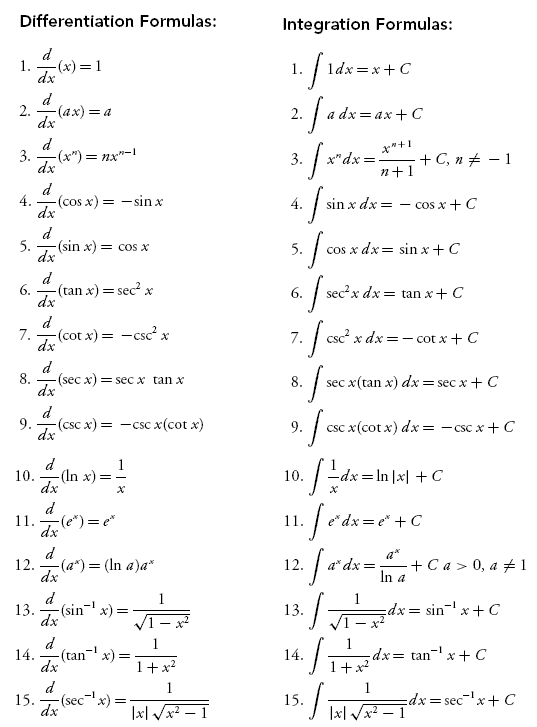
Formula 3 & 4
4. Trigonometric Twists and Turns
Moving on to the trigonometric functions, we have the integrals of sine and cosine. These are fundamental in many areas of physics and engineering, especially when dealing with oscillations and waves. The integral of sin(x) is -cos(x) + C, and the integral of cos(x) is sin(x) + C. Pay close attention to the signs! It's very easy to get them mixed up. Think of it this way: the derivative of cos(x) is -sin(x), so the integral of sin(x) must be -cos(x).
These formulas are direct consequences of the derivatives of sine and cosine. Remember that integration is the reverse process of differentiation. So, if you know the derivatives of these trigonometric functions, you'll have no trouble remembering their integrals. Just keep in mind the sign changes. One way to remember is to think about the circle. As you move counter-clockwise around the unit circle, sine turns into cosine, and cosine turns into -sine and -sine turns into -cosine and -cosine turns into sine, so the integral of sine would naturally be negative cosine. It's all connected!
Let's look at some examples. Suppose we want to integrate 3sin(x) dx. We can pull the constant 3 out of the integral, so we have 3sin(x) dx = -3cos(x) + C. Similarly, if we want to integrate 5cos(x) dx, we have 5cos(x) dx = 5sin(x) + C. These are straightforward applications of the formulas, but they're essential building blocks for solving more complex trigonometric integrals.
These formulas might seem simple, but they are the foundation for integrating a wide range of trigonometric functions. They are also crucial in solving differential equations involving oscillations and waves. So, make sure you have these formulas ingrained in your memory. Practice applying them to various examples and try to relate them to the derivatives of sine and cosine. The better you understand the connection between differentiation and integration, the easier it will be to master these trigonometric integrals.
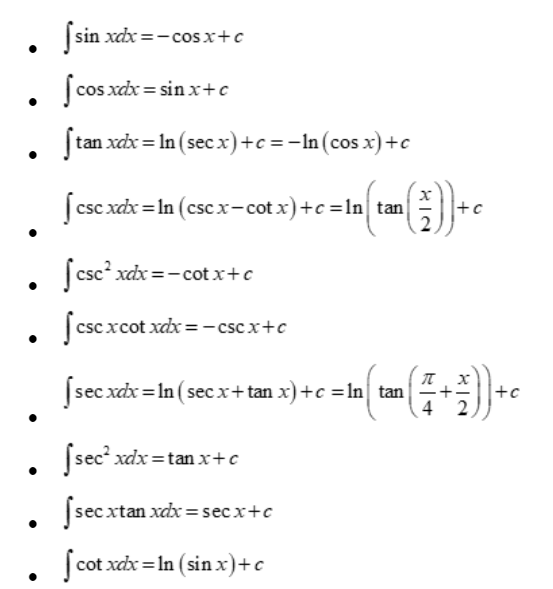
Formula 5
5. e to the Power of Awesome
Last but not least, we have the integral of ex. This is arguably the simplest of all the integration formulas. The integral of ex is simply ex + C. That's it! No sign changes, no fractions, just ex + C. It's like the mathematical equivalent of a perfect score on a test.
Why is this the case? Because the derivative of ex is also ex. This makes ex a very special function in calculus. It's its own derivative and its own integral (up to a constant, of course). This property makes it incredibly useful in modeling exponential growth and decay, which occur in various fields, from population dynamics to radioactive decay.
Let's look at an example. Suppose we want to integrate 7ex dx. We can pull the constant 7 out of the integral, so we have 7ex dx = 7ex + C. Another example, (ex + x2) dx = ex + (x3)/3 + C. We can simply integrate each term separately and add the results.
While this formula might seem almost too easy, it's incredibly powerful. The exponential function appears everywhere in mathematics and its applications. Understanding its integral is crucial for solving a wide range of problems. So, don't underestimate the importance of this simple formula. It's a cornerstone of calculus and a gateway to understanding more complex exponential functions and their applications.

Integration Formulas (in PDF) With All + Practice Questions
Putting it All Together
6. Becoming an Integration Master
So, there you have it: the five basic integration formulas. Armed with these tools, you're ready to tackle a wide range of integration problems. But remember, knowledge is only half the battle. The other half is practice! The more you practice applying these formulas, the more comfortable and confident you'll become. Start with simple examples and gradually work your way up to more challenging ones. Don't be afraid to make mistakes; they're a natural part of the learning process.
Consider these formulas as the foundation upon which more advanced integration techniques are built. Understanding these five provides a significant head-start when tackling u-substitution, integration by parts, and trigonometric substitution — all of which expand upon these core principles. It's like understanding basic chord progressions before you try to write a symphony.
And remember, calculus isn't just about memorizing formulas and applying them mechanically. It's about understanding the underlying concepts and using them to solve real-world problems. Think about how integration can be used to calculate areas, volumes, probabilities, and many other things. The more you connect the abstract concepts to concrete applications, the more meaningful and engaging calculus will become.
Don't get discouraged if you struggle at first. Integration can be challenging, even for experienced mathematicians. The key is to be patient, persistent, and to keep practicing. And remember, there are plenty of resources available to help you along the way, including textbooks, online tutorials, and knowledgeable friends or instructors. So, don't be afraid to ask for help when you need it. Together, these five formulas can unlock a new world of mathematical understanding!